TEORIA DAS ESTRUTURAS I
Determine a faixa de trabalho devido às envoltórias nas seções da viga biapoiada representada na figura abaixo. A mesma está sob um carregamento permanente de 20 KN/m e de um trem-tipo, conforme ilustrado:
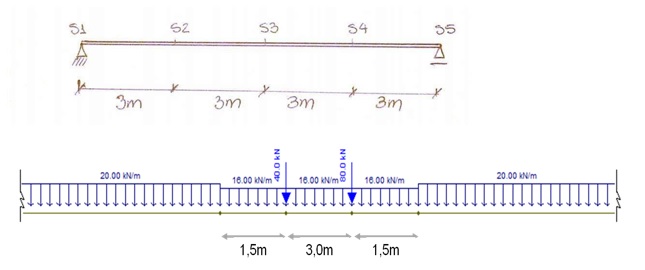
Calcule as reações nos apoios da viga devidas a carga permanente de 20 KN/m. A resposta correta é Va=Vb que vale:
30 kN
270 kN
60 kN
120 kN
240 kN
A partir das linhas de influência do momento fletor da figura abaixo, correspondentes às posições críticas do trem-tipo, os momentos Máximos nas seções S1 e S2 valem, respectivamente:

424,12 e 610,5 KN.m
483,33 e 704,42 KN.m
453,33 e 804,42 KN.m
438,00 e 604,88 KN.m
469,50 e 610,50 KN.m
Com base no pórtico ilustrado abaixo marque o valor do cortante no ponto D do trecho DE:
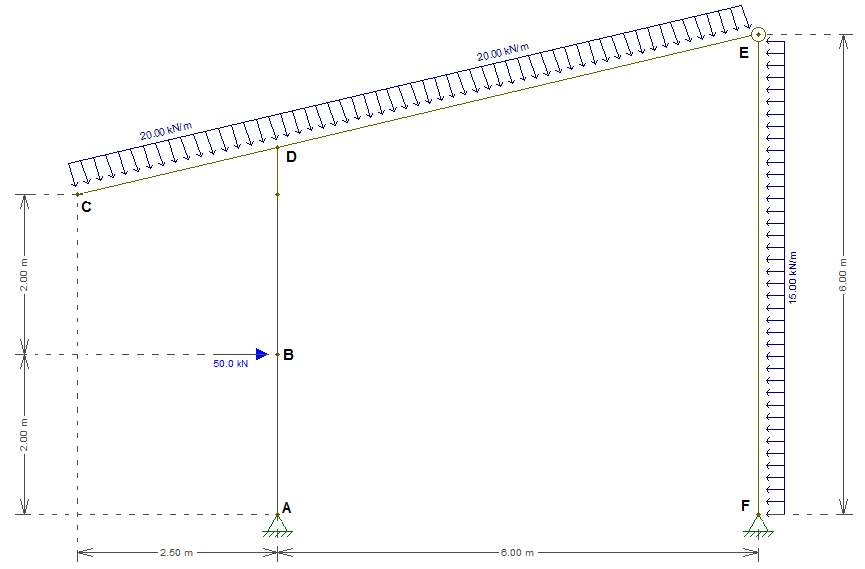
115,4 kN
45 kN
63,4 kN
51,4 kN
58,8 kN
Utilizando a estrutura de concreto armado com seção 20x50, representada na figura abaixo, determine o valor da reação no apoio G, vertical e horizontal nesta sequência e em módulo.
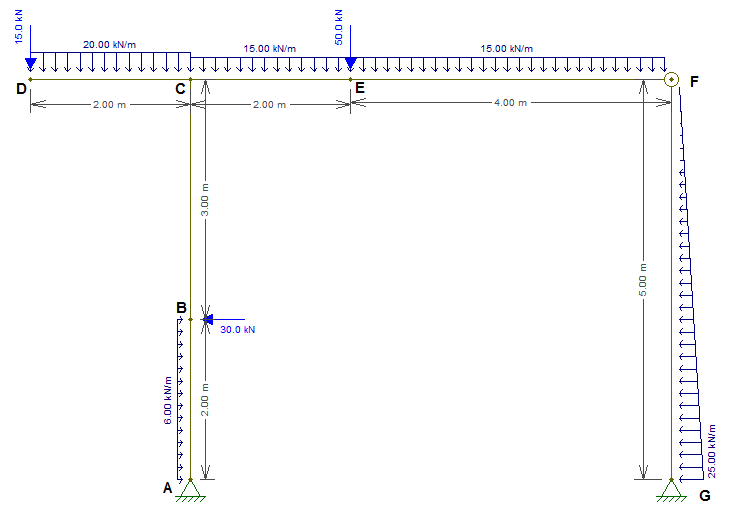
153,00 kN e 18,00 kN
170,40 kN e 38,80 kN
41,70 kN e 24,60 kN
38,00 kN e 153,00 kN
24,60 kN e 41,70 kN
Qual e o maior valor da forca cortante,em módulo, no trecho horizontal da estrutura abaixo?

14,4 kN
10,6 kN
15,7 kN
3,2 kN
8,3 kN
Qual e o valor da forca normal no trecho vertical da estrutura abaixo?

8,3 kN tração
10,6 kN tração
15,7 kN tração
14,4 kN compressão
3,2 kN compressão
Qual e o maior valor de momentos (positivo e negativo) nesta ordem e em modulo, da estrutura abaixo?
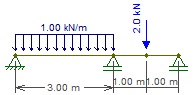
0,5 kNm e 0,7 kNm.
0,7 kNm e 0,7 kNm.
0,5 kNm e 1,0 kNm.
1,0 kNm e 0,7 kNm.
0,7 kNm e 1,0 kNm.
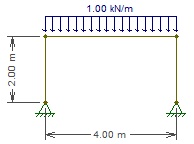
Qual o valor do maior esforço normal da estrutura representada na figura abaixo, e verifique se este esforço e de tração ou compressão?
0,5 compressão
2,0 compressão
2,0 tração
0,5 tração
2,0 tração e 0,5 de compressão
Leia os seguintes tópicos abaixo:
I - Rompe-se o vínculo capaz de transmitir o efeito E cuja linha de influência se deseja determinar;
II - Na seção onde atua o efeito E, atribui-se à estrutura, no sentido oposto ao de E positivo, um deslocamento generalizado unitário, que será tratado como sendo muito pequeno;
III - Configuração deformada (elástica) obtida é a linha de influência.
Segundo (SÜSSEKIND, 1980) deve-se seguir três etapas para traçar as LI pelo Método de Müller-Breslau, dos métodos listados nos tópicos acima está (ão) correto (s):

30 kN
270 kN
60 kN
120 kN
240 kN
A partir das linhas de influência do momento fletor da figura abaixo, correspondentes às posições críticas do trem-tipo, os momentos Máximos nas seções S1 e S2 valem, respectivamente:

424,12 e 610,5 KN.m
483,33 e 704,42 KN.m
453,33 e 804,42 KN.m
438,00 e 604,88 KN.m
469,50 e 610,50 KN.m
Com base no pórtico ilustrado abaixo marque o valor do cortante no ponto D do trecho DE:

115,4 kN
45 kN
63,4 kN
51,4 kN
58,8 kN
Utilizando a estrutura de concreto armado com seção 20x50, representada na figura abaixo, determine o valor da reação no apoio G, vertical e horizontal nesta sequência e em módulo.

153,00 kN e 18,00 kN
170,40 kN e 38,80 kN
41,70 kN e 24,60 kN
38,00 kN e 153,00 kN
24,60 kN e 41,70 kN
Qual e o maior valor da forca cortante,em módulo, no trecho horizontal da estrutura abaixo?

14,4 kN
10,6 kN
15,7 kN
3,2 kN
8,3 kN
Qual e o valor da forca normal no trecho vertical da estrutura abaixo?

8,3 kN tração
10,6 kN tração
15,7 kN tração
14,4 kN compressão
3,2 kN compressão
Qual e o maior valor de momentos (positivo e negativo) nesta ordem e em modulo, da estrutura abaixo?

0,5 kNm e 0,7 kNm.
0,7 kNm e 0,7 kNm.
0,5 kNm e 1,0 kNm.
1,0 kNm e 0,7 kNm.
0,7 kNm e 1,0 kNm.
Qual o valor do maior esforço normal da estrutura representada na figura abaixo, e verifique se este esforço e de tração ou compressão?

0,5 compressão
2,0 compressão
2,0 tração
0,5 tração
2,0 tração e 0,5 de compressão
Leia os seguintes tópicos abaixo:
I - Rompe-se o vínculo capaz de transmitir o efeito E cuja linha de influência se deseja determinar;
II - Na seção onde atua o efeito E, atribui-se à estrutura, no sentido oposto ao de E positivo, um deslocamento generalizado unitário, que será tratado como sendo muito pequeno;
III - Configuração deformada (elástica) obtida é a linha de influência.
Segundo (SÜSSEKIND, 1980) deve-se seguir três etapas para traçar as LI pelo Método de Müller-Breslau, dos métodos listados nos tópicos acima está (ão) correto (s):
424,12 e 610,5 KN.m
483,33 e 704,42 KN.m
453,33 e 804,42 KN.m
438,00 e 604,88 KN.m
469,50 e 610,50 KN.m
Com base no pórtico ilustrado abaixo marque o valor do cortante no ponto D do trecho DE:

115,4 kN
45 kN
63,4 kN
51,4 kN
58,8 kN
Utilizando a estrutura de concreto armado com seção 20x50, representada na figura abaixo, determine o valor da reação no apoio G, vertical e horizontal nesta sequência e em módulo.

153,00 kN e 18,00 kN
170,40 kN e 38,80 kN
41,70 kN e 24,60 kN
38,00 kN e 153,00 kN
24,60 kN e 41,70 kN
Qual e o maior valor da forca cortante,em módulo, no trecho horizontal da estrutura abaixo?

14,4 kN
10,6 kN
15,7 kN
3,2 kN
8,3 kN
Qual e o valor da forca normal no trecho vertical da estrutura abaixo?

8,3 kN tração
10,6 kN tração
15,7 kN tração
14,4 kN compressão
3,2 kN compressão
Qual e o maior valor de momentos (positivo e negativo) nesta ordem e em modulo, da estrutura abaixo?

0,5 kNm e 0,7 kNm.
0,7 kNm e 0,7 kNm.
0,5 kNm e 1,0 kNm.
1,0 kNm e 0,7 kNm.
0,7 kNm e 1,0 kNm.
Qual o valor do maior esforço normal da estrutura representada na figura abaixo, e verifique se este esforço e de tração ou compressão?

0,5 compressão
2,0 compressão
2,0 tração
0,5 tração
2,0 tração e 0,5 de compressão
Leia os seguintes tópicos abaixo:
I - Rompe-se o vínculo capaz de transmitir o efeito E cuja linha de influência se deseja determinar;
II - Na seção onde atua o efeito E, atribui-se à estrutura, no sentido oposto ao de E positivo, um deslocamento generalizado unitário, que será tratado como sendo muito pequeno;
III - Configuração deformada (elástica) obtida é a linha de influência.
Segundo (SÜSSEKIND, 1980) deve-se seguir três etapas para traçar as LI pelo Método de Müller-Breslau, dos métodos listados nos tópicos acima está (ão) correto (s):

115,4 kN
45 kN
63,4 kN
51,4 kN
58,8 kN
Utilizando a estrutura de concreto armado com seção 20x50, representada na figura abaixo, determine o valor da reação no apoio G, vertical e horizontal nesta sequência e em módulo.

153,00 kN e 18,00 kN
170,40 kN e 38,80 kN
41,70 kN e 24,60 kN
38,00 kN e 153,00 kN
24,60 kN e 41,70 kN
Qual e o maior valor da forca cortante,em módulo, no trecho horizontal da estrutura abaixo?

14,4 kN
10,6 kN
15,7 kN
3,2 kN
8,3 kN
Qual e o valor da forca normal no trecho vertical da estrutura abaixo?

8,3 kN tração
10,6 kN tração
15,7 kN tração
14,4 kN compressão
3,2 kN compressão
Qual e o maior valor de momentos (positivo e negativo) nesta ordem e em modulo, da estrutura abaixo?

0,5 kNm e 0,7 kNm.
0,7 kNm e 0,7 kNm.
0,5 kNm e 1,0 kNm.
1,0 kNm e 0,7 kNm.
0,7 kNm e 1,0 kNm.
Qual o valor do maior esforço normal da estrutura representada na figura abaixo, e verifique se este esforço e de tração ou compressão?

0,5 compressão
2,0 compressão
2,0 tração
0,5 tração
2,0 tração e 0,5 de compressão
Leia os seguintes tópicos abaixo:
I - Rompe-se o vínculo capaz de transmitir o efeito E cuja linha de influência se deseja determinar;
II - Na seção onde atua o efeito E, atribui-se à estrutura, no sentido oposto ao de E positivo, um deslocamento generalizado unitário, que será tratado como sendo muito pequeno;
III - Configuração deformada (elástica) obtida é a linha de influência.
Segundo (SÜSSEKIND, 1980) deve-se seguir três etapas para traçar as LI pelo Método de Müller-Breslau, dos métodos listados nos tópicos acima está (ão) correto (s):

153,00 kN e 18,00 kN
170,40 kN e 38,80 kN
41,70 kN e 24,60 kN
38,00 kN e 153,00 kN
24,60 kN e 41,70 kN
Qual e o maior valor da forca cortante,em módulo, no trecho horizontal da estrutura abaixo?

14,4 kN
10,6 kN
15,7 kN
3,2 kN
8,3 kN
Qual e o valor da forca normal no trecho vertical da estrutura abaixo?

8,3 kN tração
10,6 kN tração
15,7 kN tração
14,4 kN compressão
3,2 kN compressão
Qual e o maior valor de momentos (positivo e negativo) nesta ordem e em modulo, da estrutura abaixo?

0,5 kNm e 0,7 kNm.
0,7 kNm e 0,7 kNm.
0,5 kNm e 1,0 kNm.
1,0 kNm e 0,7 kNm.
0,7 kNm e 1,0 kNm.
Qual o valor do maior esforço normal da estrutura representada na figura abaixo, e verifique se este esforço e de tração ou compressão?

0,5 compressão
2,0 compressão
2,0 tração
0,5 tração
2,0 tração e 0,5 de compressão
Leia os seguintes tópicos abaixo:
I - Rompe-se o vínculo capaz de transmitir o efeito E cuja linha de influência se deseja determinar;
II - Na seção onde atua o efeito E, atribui-se à estrutura, no sentido oposto ao de E positivo, um deslocamento generalizado unitário, que será tratado como sendo muito pequeno;
III - Configuração deformada (elástica) obtida é a linha de influência.
Segundo (SÜSSEKIND, 1980) deve-se seguir três etapas para traçar as LI pelo Método de Müller-Breslau, dos métodos listados nos tópicos acima está (ão) correto (s):

14,4 kN
10,6 kN
15,7 kN
3,2 kN
8,3 kN
Qual e o valor da forca normal no trecho vertical da estrutura abaixo?

8,3 kN tração
10,6 kN tração
15,7 kN tração
14,4 kN compressão
3,2 kN compressão
Qual e o maior valor de momentos (positivo e negativo) nesta ordem e em modulo, da estrutura abaixo?

0,5 kNm e 0,7 kNm.
0,7 kNm e 0,7 kNm.
0,5 kNm e 1,0 kNm.
1,0 kNm e 0,7 kNm.
0,7 kNm e 1,0 kNm.
Qual o valor do maior esforço normal da estrutura representada na figura abaixo, e verifique se este esforço e de tração ou compressão?

0,5 compressão
2,0 compressão
2,0 tração
0,5 tração
2,0 tração e 0,5 de compressão
Leia os seguintes tópicos abaixo:
I - Rompe-se o vínculo capaz de transmitir o efeito E cuja linha de influência se deseja determinar;
II - Na seção onde atua o efeito E, atribui-se à estrutura, no sentido oposto ao de E positivo, um deslocamento generalizado unitário, que será tratado como sendo muito pequeno;
III - Configuração deformada (elástica) obtida é a linha de influência.
Segundo (SÜSSEKIND, 1980) deve-se seguir três etapas para traçar as LI pelo Método de Müller-Breslau, dos métodos listados nos tópicos acima está (ão) correto (s):

8,3 kN tração
10,6 kN tração
15,7 kN tração
14,4 kN compressão
3,2 kN compressão
Qual e o maior valor de momentos (positivo e negativo) nesta ordem e em modulo, da estrutura abaixo?

0,5 kNm e 0,7 kNm.
0,7 kNm e 0,7 kNm.
0,5 kNm e 1,0 kNm.
1,0 kNm e 0,7 kNm.
0,7 kNm e 1,0 kNm.
Qual o valor do maior esforço normal da estrutura representada na figura abaixo, e verifique se este esforço e de tração ou compressão?

0,5 compressão
2,0 compressão
2,0 tração
0,5 tração
2,0 tração e 0,5 de compressão
Leia os seguintes tópicos abaixo:
I - Rompe-se o vínculo capaz de transmitir o efeito E cuja linha de influência se deseja determinar;
II - Na seção onde atua o efeito E, atribui-se à estrutura, no sentido oposto ao de E positivo, um deslocamento generalizado unitário, que será tratado como sendo muito pequeno;
III - Configuração deformada (elástica) obtida é a linha de influência.
Segundo (SÜSSEKIND, 1980) deve-se seguir três etapas para traçar as LI pelo Método de Müller-Breslau, dos métodos listados nos tópicos acima está (ão) correto (s):

0,5 kNm e 0,7 kNm.
0,7 kNm e 0,7 kNm.
0,5 kNm e 1,0 kNm.
1,0 kNm e 0,7 kNm.
0,7 kNm e 1,0 kNm.
Qual o valor do maior esforço normal da estrutura representada na figura abaixo, e verifique se este esforço e de tração ou compressão?

0,5 compressão
2,0 compressão
2,0 tração
0,5 tração
2,0 tração e 0,5 de compressão
Leia os seguintes tópicos abaixo:
I - Rompe-se o vínculo capaz de transmitir o efeito E cuja linha de influência se deseja determinar;
II - Na seção onde atua o efeito E, atribui-se à estrutura, no sentido oposto ao de E positivo, um deslocamento generalizado unitário, que será tratado como sendo muito pequeno;
III - Configuração deformada (elástica) obtida é a linha de influência.
Segundo (SÜSSEKIND, 1980) deve-se seguir três etapas para traçar as LI pelo Método de Müller-Breslau, dos métodos listados nos tópicos acima está (ão) correto (s):

0,5 compressão
2,0 compressão
2,0 tração
0,5 tração
2,0 tração e 0,5 de compressão